Sorting Techniques
Using the built in sort is okay with small data is okay. But when it comes to big data the built in sort is very expensive, the Big O!
Sorting is arranging data in a particular format. Sorting algorithms specifies the way to arrange data order. Most are in numerical or lexicographical order.
A type of Sorting is said to happen “in-place sorting” when the algorithm does not require any extra space, for example bubble-sort. Other sorting algorithms require space equal or more than the algorithm elements, this is called not-in-place sorting. For example, merge sort.
Moreover, there is stable and not stable sorting. Stable sorting does not change the sequence of duplicate value in which they appear, while unstable sorting changes the sequence of duplicate content.
Furthermore, there are adaptive and non-adaptive sorting algorithms. An adaptive sorting algorithm takes into account that some elements might be already sorted in the list. A non-adaptive sorting algorithm does not take into account that some lists are already sorted, and re-enforces sorting to confirm the sort. Example: 1, 3, 4, 6, 8, 9
An increasing order is if the successive element is great than the previous one.
A non-decreasing order is if the successive element is greater than or equal to the previous element in the sequence. Example: 1, 3, 3, 6, 8, 9
A decreasing order is when successive element is less than the current one.
A non-increasing order if the successive element is less than or equal to its previous element in the sequence
Check https://www.toptal.com/developers/sorting-algorithms to get a taste of how some of these sorting algorithms work
Stable Sorting Algorithms:
Insertion Sort Merge Sort Bubble Sort
Unstable Sorting Algorithms:
Selection sort Shell sort Quick sort
Bubble Sort
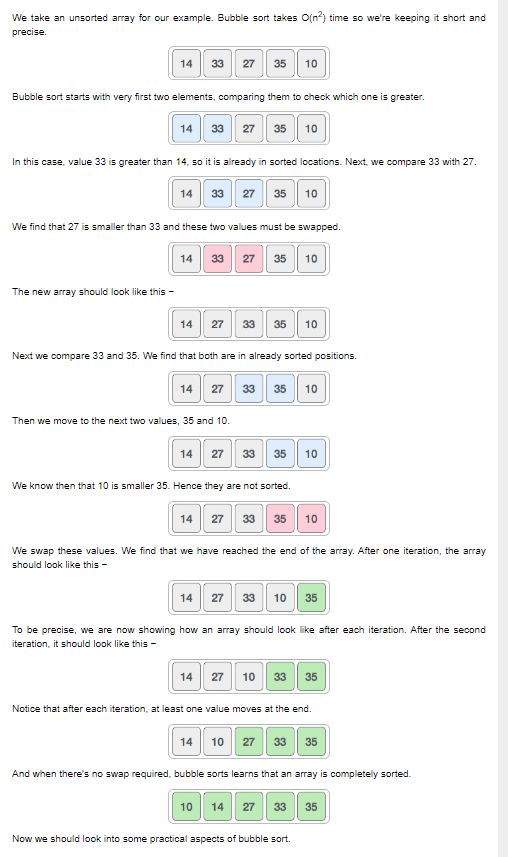
o It is a simple algorithm which compares a pair of adjacent elements and swaps them if they are not equal. Bubble sort starts with the first two elements, compares them to check which is greater, then swaps them. It keeps on repeating this process until no swaps are required by the last pass
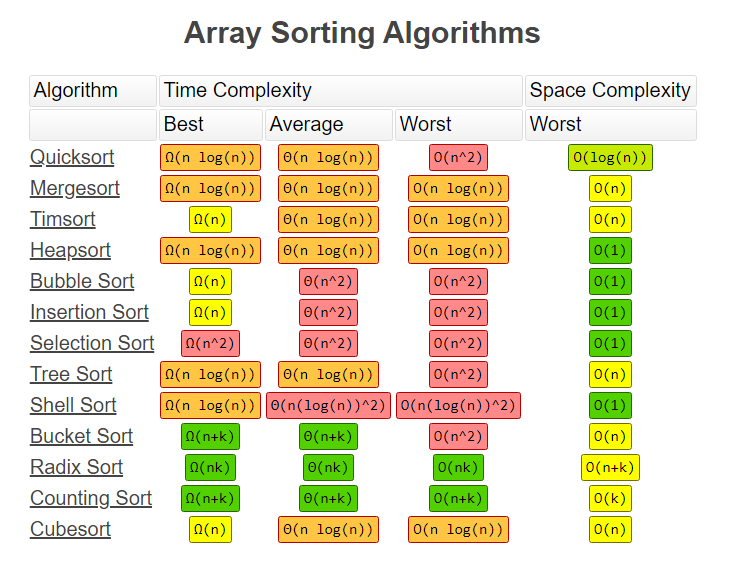
o This algorithm is not suitable for large scale data sets and the worst case complexity are O(n^2) where n is the number of items
Selection Sort
o This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left and the unsorted part at the right side. Initially, the sorted part is empty, and the unsorted part is the entire list. o Selection sort finds the lowest number on every iteration o The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes part of the sorted array. This process continues moving unsorted array by one element to the right. Not suitable for large datasets with a worse case complexity are of O(n^2), where n is the number of items.
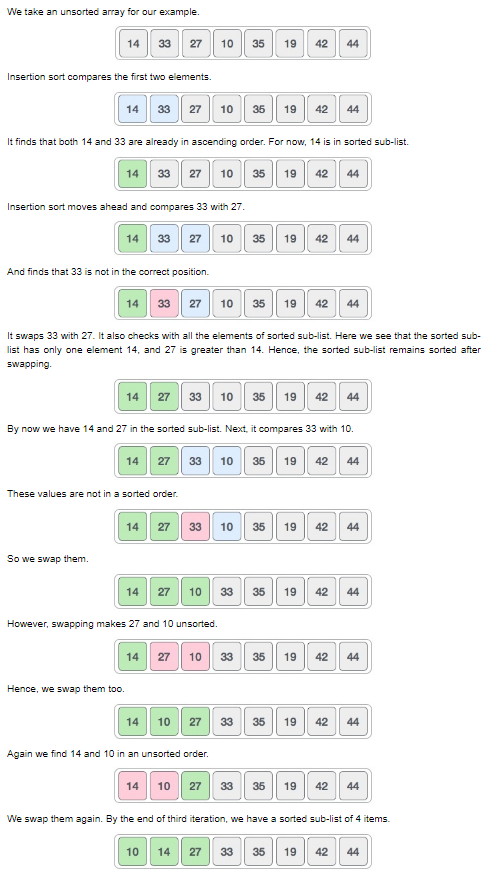
Insertion Sort
o This is an in-place comparison-based sorting algorithm. A sorted sub-list is maintained which is always sorted. An element which is to be “insert”ed in this sorted sub-list, has to find its appropriate place and then it has to be inserted there. The array is search sequentially and unsorted items are moved and inserted into the sorted sub-list. o Not suitable for large data since the worse case complexity are O(n^2) where n is the number of items. o Insertion sorts, scans number by number and inserts it in the appropriate place on the sorted array o Good reference: https://stackoverflow.com/questions/15799034/insertion-sort-vs-selection-sort
Merge Sort
- Idea is based on divide and conquer technique with a worse-case time complexity being O(n log n).
- Merge sort divides the whole array iteratively unless the atomic values are achieved. The elements for each list are compared and combined in a sorted manner. And recursively lists are merged, until the list is back again.
The input array is divided several times, sorted and then they are combined and merged back together. That is O(nlog(n)) in time complexity which is known as linearithmic. It is the same with best, average or worse scenario since the amount of operations are still the same. For space complexity, the number of levels represents the recursion, if we double the data, we need one more level of recursion, therefore, the stack will increase logarithmically. So the stack has O(log n) space complexity but the auxiliary array has O(n) linear space complexity, since you need temporary stacks to hold the array. Since linear complexity is bigger, than the space complexity of merge sort is linear.
Quick sort
- Also based on the divide and conquer algorithm
- Is a highly efficient sorting algorithm and is based on partitioning of array into smaller arrays. It is based on the divide-and-conquer algorithm.
- The large array is partitioned into two arrays, one of which holds values smaller than the specified value, say pivot. Based on that partition values will hold greater or smaller values.
- The pivot value divides the list into two parts and recursively, it finds the pivot for each sub-lists until all lists contain only one element _ There are four ways the pivot can be picked, the first element as a pivot, the last element as a pivot, a random element as a pivot and a median element as a pivot. _ The pivot should divide the list where all elements smaller than it should go to the left side, and all elements larger than it should go on the right side.
Example: Choose the highest index to be the pivot Take two variables to point left and right of the list excluding pivot Left points to the low index Right points to the high index While value at left is less than pivot move right While value at right is greater than pivot move left If both steps 5 and steps 6 does not match swap left and right If left is bigger than right, the point where they met is the new pivot
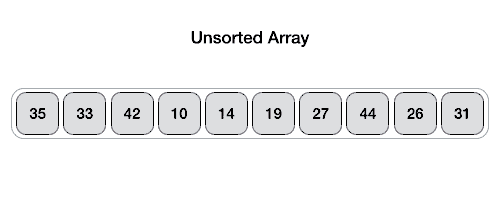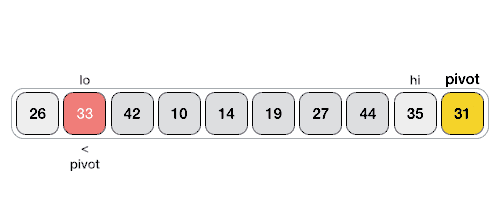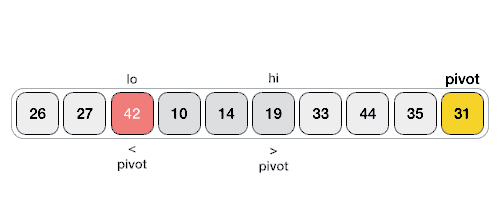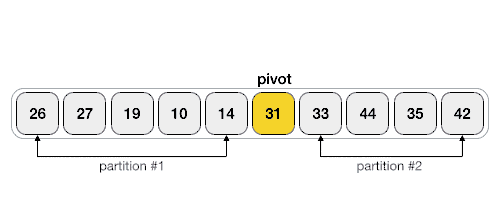
Quick sort and merge sort, are the most common used.
Shell Sort
o Based on the insertion sort algorithm but highly efficient. Shell sorts avoids large shifts as in case of insertion sort, if the smaller value is to the far right and has to be moved to the far left. o It uses spacing termed as interval which is calculated based on the Knuth’s formulae. o The worse case is O(n) since it depends on the gap sequence o The concept of gap is if it i.e. equals to 4, then we will consider the first element and the 5th element. The 2nd element with 6th element and so on. We compare these numbers and sort them. We then create a smaller gap for example 2 and again swap values according to the other. o In the last pass shell sort is like the insertion sort with gap 1. Where it compares element next to each other.
This algorithm uses insertion sort on a widely spread elements, first to sort them and then sorts the less widely spaced elements. This spacing is termed as interval. This interval is calculated based on Knuth’s formula as −
1
2
3
h = h * 3 + 1
where −
h is interval with initial value 1
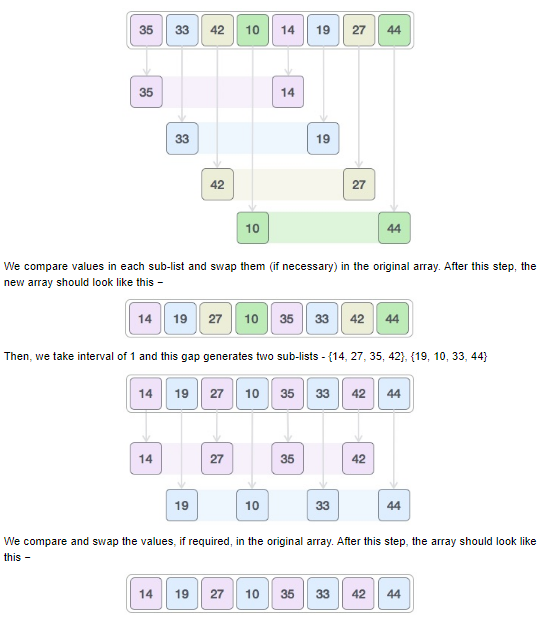
Heap Sort
A good illustration of heap sort is here https://brilliant.org/wiki/heap-sort/
Non comparison Sort
Radix Sort and Counting Sort are strictly for a numbers within a certain range and length.
Stable vs not stable algorithms example
A stable sorting algorithm is the one that sorts the identical elements in their same order as they appear in the input, whilst unstable sorting may not satisfy the case. - I thank my algorithm lecturer Didem Gozupek to have provided insight into algorithms.
Radix Sort: https://brilliant.org/wiki/radix-sort/
Radix Sort Animation: https://www.cs.usfca.edu/~galles/visualization/RadixSort.html
Counting Sort: https://brilliant.org/wiki/counting-sort/
Counting Sort Animation: https://www.cs.usfca.edu/~galles/visualization/CountingSort.html
Summarize
Practice Questions
1 - Sort 10 schools around your house by distance: Insertion Sort, small data and fast, with low space complexity.
2 - eBay sorts listings by the current Bid amount: Radix or counting sort, since the data is fixed length of integers with a fixed range.
3 - Sport scores on ESPN: Quick sort, since there is so many types of sports and so many types of games to keep track off.
4 - Massive database (can’t fit all into memory) needs to sort through past year’s user data: MergeSort, it will be sorted out of memory, and we need good performance.
5 - Almost sorted Udemy review data needs to update and add 2 new reviews: Insertion Sort
6 - Temperature Records for the past 50 years in Canada: Quick Sort, to do in memory sorting and save space time complexity.
7 - Large user name database needs to be sorted. Data is very random: MergeSort if we have enough memory and memory is not expensive. or use QuickSort if I am not too worried about the worse case scenerio
8 - You want to teach sorting for the first time: Bubble Sort or Selection Sort