Linear Search
A sequential search is made over all items one by one. Every item is checked and if a match is found then the item is returned. Otherwise, the search continues to the end. with O(n) complexity since in worse case it has to search all the data in array.
Binary Search
Is a fast algorithm with a run-time complexity of O(log n). This search algorithm works on the principle of divide and conquer. The items should be already sorted. The binary target looks for the item in the middle most item of the collection. If the match occurs, the index is returned otherwise, the middle item is great than the item it will search the sub-array to the left or right. In the sub-array, the mid index again checked if it contains the value. If not, it is subdivided and if smaller than mid value, the left side is checked, otherwise the right side will be checked. The search is continued until the subarray is reduced to zero.
Interpolation Search
An improved variant of binary search. The search algorithm works on the probing position of the required value. For this algorithm to work properly, the data collection should be in a sorted form and equally distributed.
Binary search goes to the middle element to check the algorithm. It does not take advantage to probe the position of the desired data. On the other hand, interpolation search searches in different locations according to the value of the key being searched. If the value of the key is close to the last element, interpolation search will start at the end. The interpolation search uses this equation instead to start looking for the index instead of jumping straight to the middle.
1
2
3
4
5
6
7
8
9
mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo])
Step 1 − Start searching data from middle of the list.
Step 2 − If it is a match, return the index of the item, and exit.
Step 3 − If it is not a match, probe position.
Step 4 − Divide the list using probing formula and find the new midle.
Step 5 − If data is greater than middle, search in higher sub-list.
Step 6 − If data is smaller than middle, search in lower sub-list.
Step 7 − Repeat until match.
Depth First Traversal
This is O(n) since we have to visit all the nodes.
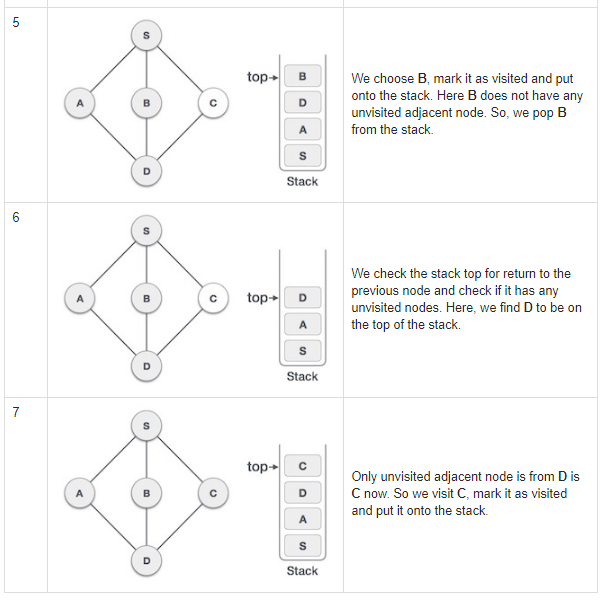
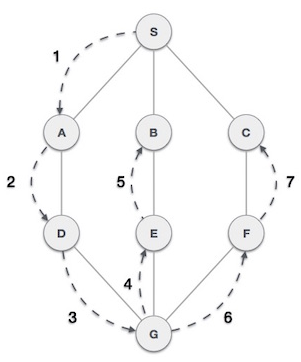
Depth first traversal traverses a graph in a depthward motion and uses a stack to remember to get to the next vertex to start a search, when a dead end occurs in any iteration. So a depth first travel, follows a path from a starting vertex until we reach the end of the vertex on that track. It then goes back an iteration and visits all the neighboring path in that vertex, and so on, until there are no longer any vertices to cover. We backtrack until all have been visited. dfs.
It uses less memory than BFS since it does need memory to save child points/location.
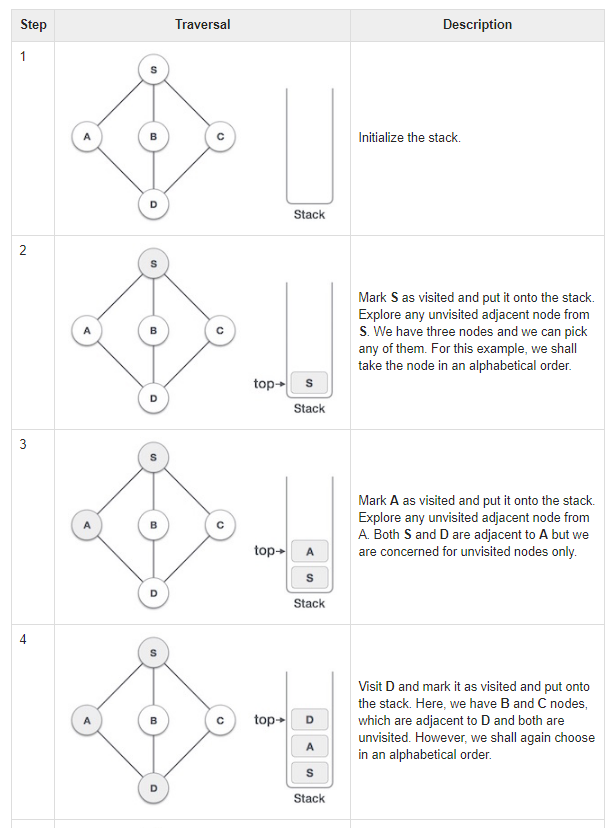
The depth first traversal algorithm:
- Push the first vertex onto the stack
- Mark this vertex as visited
- Repeat o Visit the next vertex adjacent to the one on top of the stack o Push this vertex onto the stack o Mark this vertex as visited o If there isn’t a vertex to bisit o Pop this vertex off the stack
- End
- Until the stack is empty
DFS uses stacking whils BFS uses queuing.
Breadth First Traversal
This is O(n) since we have to visit all the nodes.
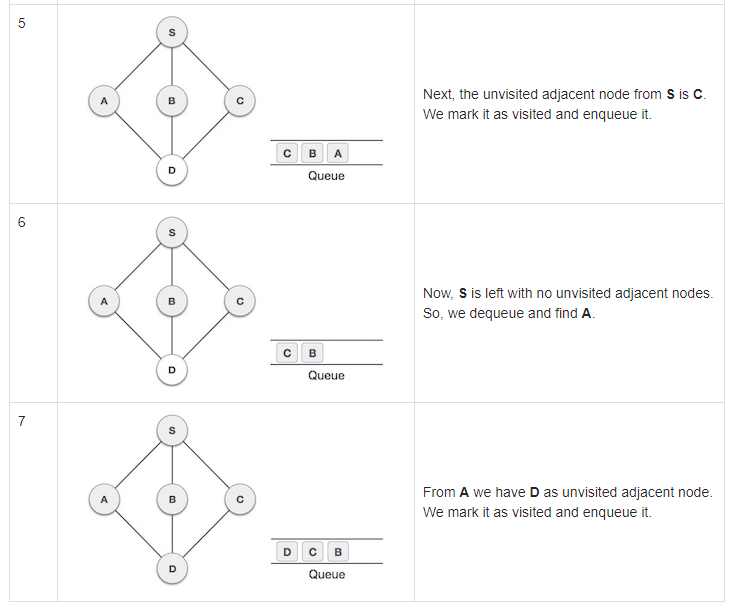
Breath first research algorithm traverses a graph in a breadthward motion and uses a queue to remember to get the next vertex to start a search, when a dead end occurs in any iteration. The BFS starts by examining the nodes closer to the vertex and gradually starts examining those further away from the vertex.
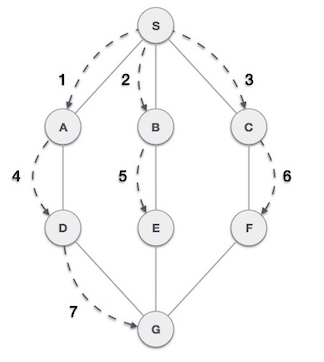
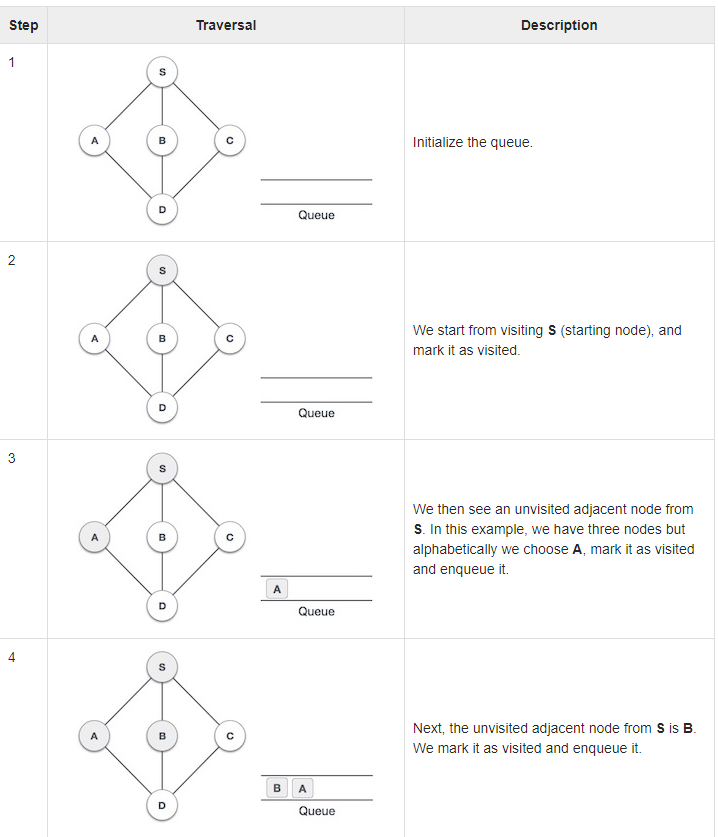
Rule 1: visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue.
Rule 2: If no adjacent vertex is found, remove the first vertex from the queue
Rule 3: Repeat rule 1 and rule 2 until the queue is empty
You keep on going left to right until all nodes have been visited and dequeued. In other words, when there are no unmarked (unvisited) nodes. But as per the algorithm we keep on dequeuing in order to get all unvisited nodes. When the queue gets emptied, the program is over.
Both of these methods can be used in Graphs or Trees.
Breadth First Traversal vs Depth First Traversal
BFS downside it requires more memory than DFS. All of the connected vertices must be stored in memory. So consumes more memory The upside is, if you know the information required is closer up the node, then BFS will find it faster than DFS. Furthermore, it finds the shortest path between vertices
The DFS is better if solutions are frequent and located deep in the tree, or whether a path exists between two nodes, if the tree is wide (since BFS will require alot of memory). Moreover, DFS consumes less memory and finds the larger distant element(from source vertex) in less time.
THE BFS is better when you need to find the shortest path, know the solution is closer to the root, if the solution is very deep but are rare.