Recursions

Recursion

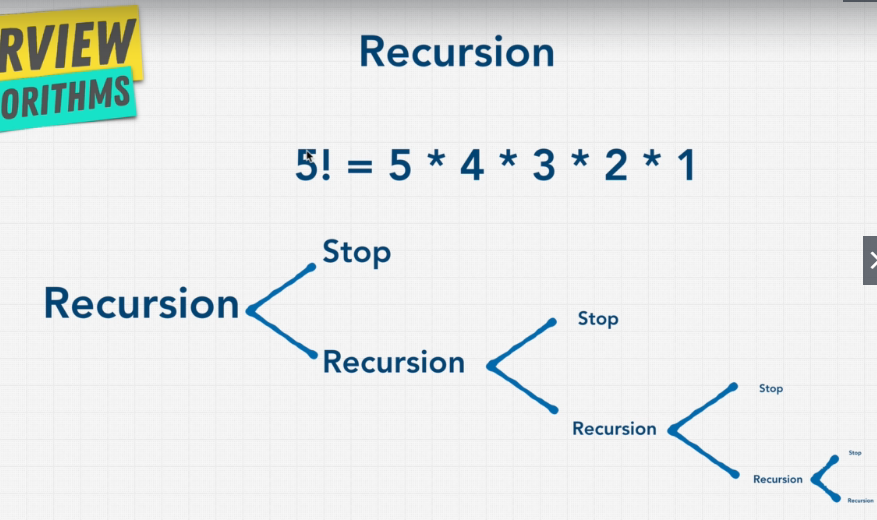
A recursion is where a function calls itself directly, or calls a function to call it directly. A recursive function can go infinite like a loop, therefore there must be 2 conditions.

Stackoverflow: is when the function call itself indefinetely leading to the over-filling if the stack size, and crashing it. This is because nothing gets popped from the stack. And memory is limited, leading to stackoverflow.

The base criteria: There must be at least one base criteria or condition, such that, when this condition is met the function stops calling itself recursively.

The Progression Approach: The recursive calls should progress in such a way that each time a recursive call is made it comes closer to the base criteria.

Implementation: Recursion is implemented by means of stacks. The call stack holds the activation record on local variables, formal parameters, return address and all information passed to the caller function. When a function call itself, it suspends the execution temporarily and resume later when the execution control returns. The information is stored in the call stack.

Analysis of Recursion: Recursion makes a programmable more readable and is more efficient that iterations.

Time complexity: The number of times a recursive call is made is counted as 1. Therefore, recursion is O(n)

Space Complexity: The space complexity of recursive function may go higher than that of a function with iteration since it has to store all the data in every iteration.

Examples

Tower of Hanoi: is a puzzle which consists of three towers and atleast 3 rings. The minimal amount of moves required is 2^n -1.

def hanoi(n, source, helper, target):
    print "hanoi( ", n, source, helper, target, " called"
    if n > 0:
        # move tower of size n - 1 to helper:
        hanoi(n - 1, source, target, helper)
        # move disk from source peg to target peg
        if source[0]:
            disk = source[0].pop()
            print "moving " + str(disk) + " from " + source[1] + " to " + target[1]
            target[0].append(disk)
        # move tower of size n-1 from helper to target
        hanoi(n - 1, helper, source, target)

source = ([4,3,2,1], "source")
target = ([], "target")
helper = ([], "helper")
hanoi(len(source[0]),source,helper,target)

print source, helper, target

Fibonacci: Fibonacci series generates the subsequent number by adding two previous numbers. (insert python example with iterative algorithm and recursive algorithm.

Using recursive method

def recur_fibo(n):
   if n <= 1:
       return n
   else:
       return(recur_fibo(n-1) + recur_fibo(n-2))

Using iterative method

def fibonacci(n):
    a,b = 0,1
    for i in range(n):
        a,b = b,a+b
    return a

Recursive vs Iterative:

Anything you do with a recursion can be done iteratively (loop). When do you use recursion though ? Everytime you are using tees consider recursion. 1- Divide into a number of subproblems that are smaller instances of the same problem. 2- Each instane of the subproblem is identical in nature 3- The solutions of each subproblem can be combined to solve the problem at hand.